Evaluating Deep Learning Models with Custom Loss Functions and Calibration Metrics

Evaluating Deep Studying fashions is an important a part of mannequin lifecycle administration. Whereas conventional fashions have excelled at offering fast benchmarks for mannequin efficiency, they usually fail to seize the nuanced objectives of real-world purposes. As an illustration, a fraud detection system may prioritize minimizing false negatives over false positives, whereas a medical analysis mannequin may worth recall greater than precision. In such situations, relying solely on typical metrics can result in suboptimal mannequin habits. That is the place customized loss capabilities and tailor-made analysis metrics come into play.

Typical Deep Studying Fashions Analysis

The traditional measures to judge classification embrace Accuracy, Recall, F1-score, and so forth. Cross-entropy loss is the popular loss operate to make use of for classification. These typical measures of classification consider solely whether or not predictions have been appropriate or not, ignoring uncertainty.

A mannequin can have excessive accuracy however poor likelihood estimates. Trendy deep networks are overconfident and return chances of ~0 or ~1 even when they’re improper.

Learn extra: Typical mannequin analysis metrics

The Downside

Guo et al. present {that a} extremely correct deep mannequin can nonetheless be poorly calibrated. Likewise, a mannequin might need a excessive F1 rating however nonetheless could possibly be miscalibrated in its uncertainty estimates. Optimizing goal capabilities like accuracy or log-loss may produce miscalibrated chances, since conventional analysis metrics don’t assess whether or not the mannequin’s confidence matches actuality. As an illustration, a pneumonia detection AI may output 99.9% likelihood based mostly on patterns that additionally happen in innocent circumstances, resulting in overconfidence. Calibration strategies like temperature scaling alter these scores so that they higher mirror true likelihoods.

What Are Customized Loss Features?

A customized loss or goal operate is any coaching loss operate (apart from commonplace losses like cross-entropy and MSE) that you simply invent to precise particular objectives. You may develop one when a extra generic loss doesn’t meet your enterprise necessities. 

As an illustration, you may use a loss that penalizes false negatives, missed fraud, greater than false positives. This allows you to deal with uneven penalties or objectives, like maximizing F1 as an alternative of simply accuracy. A loss is just a easy mathematical system that compares predictions with labels, so you may design any system that intently mimics the metric or price you need.

Why construct a Customized Loss Perform?

Typically the default loss under-trains on essential instances (e.g., uncommon lessons) or doesn’t mirror your utility. Customized losses provide the capability to:

• Align with enterprise logic: e.g., penalize lacking a illness 5× greater than a false alarm.
• Deal with imbalance: downweight the bulk class, or give attention to the minority.
• Encode area heuristics: e.g., require predictions to respect monotonicity or ordering.
• Optimize for particular metrics: approximate F1/precision/recall, or domain-specific ROI.

Easy methods to Implement a Customized Loss Perform?

On this part, we’ll implement a customized loss with PyTorch utilizing the nn.Module operate. The next are its key factors:

• Differentiability: Be certain that the loss operate is differentiable for the mannequin outputs.
• Numerical Stability: Use log-sum-exp or steady capabilities in PyTorch (F.log_softmax, F.cross_entropy, and so forth.). For instance, one can write Focal Loss by utilizing F.cross_entropy (containing softmax and log) in the identical method, however then multiplying by (1−𝑝𝑡)𝛾. This methodology avoids needing to compute the possibilities in a separate softmax, which may underflow.
• Code Instance: To reveal the thought, right here is how one would outline a customized Focal Loss in PyTorch:

import torch

import torch.nn as nn

import torch.nn.practical as F

class FocalLoss(nn.Module):

   def __init__(self, gamma=2.0, weight=None):

       tremendous(FocalLoss, self).__init__()

       self.gamma = gamma

       self.weight = weight  # weight tensor for lessons (non-obligatory)

   def ahead(self, logits, targets):

       # Compute commonplace cross entropy loss per-sample

       ce_loss = F.cross_entropy(logits, targets, weight=self.weight, discount='none')

       p_t = torch.exp(-ce_loss)          # The mannequin's estimated likelihood for true class

       loss = ((1 - p_t) ** self.gamma) * ce_loss

       return loss.imply()

Right here, γ tunes how a lot focus we would like on the exhausting examples. The upper γ=extra focus, and this suggests that weight can deal with class imbalance.

We used Focal loss because the loss operate because it’s designed to deal with class imbalance in object detection and different machine studying duties, notably when coping with a lot of simply labeled examples, e.g., background in object detection. This makes it appropriate for our process. 

Why Mannequin Calibration Issues?

Calibration describes how nicely predicted chances correspond to real-world frequencies. A mannequin is well-calibrated if amongst all of the cases to which it assigns likelihood p to the constructive class, about p fraction are constructive. In different phrases, “confidence = accuracy”. As an illustration, if a mannequin predicts 0.8 on 100 check instances, we might anticipate about 80 to be appropriate. Calibration is essential when utilizing chances for a call (e.g., threat scoring; cost-benefit evaluation). Formally, which means for a classifier with a likelihood output 𝑝^, calibration is:

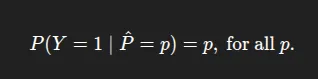
Calibration Errors

Calibration errors fall into two classes:

1. Overconfidence: Means the mannequin’s predicted chances are systematically greater than true chances (e.g., predicts 90%, however is correct 80% of the time). Deep neural networks are usually overconfident, particularly when overparameterized. Overconfident fashions may be harmful; they usually make sturdy predictions and might mislead us when misclassifying.
2. Underconfidence: Underconfidence is much less frequent in deep nets. That is the alternative of overconfidence, when the mannequin’s confidence is simply too low (e.g., predicts 60%, however is correct 80% of the time). Whereas underconfidence usually locations the mannequin in a safer place when predicting, it could look uncertain and thus much less helpful.

In follow, trendy DNNs are usually overconfident. Guo et al. discovered that newer deep nets with batch norm, deeper layers, and so forth., had spiky posterior distributions with very excessive likelihood on one class, even whereas misclassifying. Once we make these miscalibrations, it’s essential to appreciate them so we are able to make dependable predictions.

Metrics for Calibration

• Reliability Diagram: Calibration Curve Generally referred to as a reliability diagram, this additionally casts the expected successes into bins based mostly on the prediction’s confidence rating. For every bin, it plots the proportion of positives (y-axis) vs. the imply predicted likelihood on the x-axis.

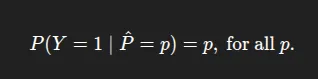
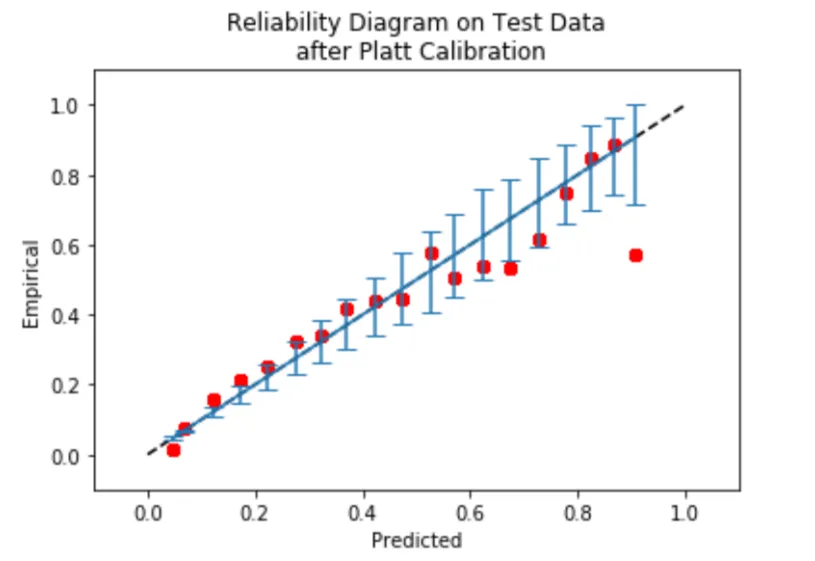
• Anticipated Calibration Error (ECE): It summarizes absolutely the distinction between accuracy and confidence, weighted by the dimensions of the bin. Formally, the place acc(b) and conf(b) are the accuracy and imply confidence in bin dimension. As a reminder, decrease values of ECE are higher (0=completely calibrated). ECE is a measure of common miscalibration. 

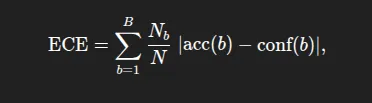
• Most Calibration Error (MCE): The biggest hole over all bins:

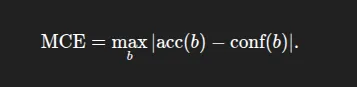
• Brier Rating: Brier rating is the imply squared error between the expected likelihood and the precise final result, which is both 0 or 1. It’s a correct scoring rule and captures each calibration and accuracy. Nevertheless, a smaller Brier rating doesn’t imply the predictions are nicely calibrated. It combines calibration and discrimination.

Learn extra: Calibration of Machine Studying Fashions

Case Research utilizing PyTorch

Right here, we’ll use the BigMart Sales dataset to reveal how the customized loss capabilities and the calibration matrices assist in predicting the goal column, OutletSales.

We modify the continual OutletSales to a binary Excessive vs Low class by thresholding on the median. We then match a easy classifier in PyTorch utilizing options comparable to product visibility, after which apply customized loss and calibration. 

Key steps

Information Preparation and Preprocessing: On this half, we’ll import the libraries, load the info, and most significantly, do the info preprocessing steps. Like lacking worth dealing with, making the specific column uniform (‘low fats’, ‘Low Fats’, and lf all are the identical so that they’ll change into “Low Fats”), making a threshold for the goal variable, performing OHE (One-hot encoding) on categorical variables, and splitting the options.

import os
import random
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

import torch
import torch.nn as nn
import torch.nn.practical as F
from torch.utils.information import TensorDataset, DataLoader, random_split

from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.utils.class_weight import compute_class_weight


SEED = 42
random.seed(SEED)
np.random.seed(SEED)
torch.manual_seed(SEED)

if torch.cuda.is_available():
    torch.cuda.manual_seed_all(SEED)

system = torch.system('cuda' if torch.cuda.is_available() else 'cpu')
print('Machine:', system)

# ----- missing-value dealing with -----
df['Weight'].fillna(df['Weight'].imply(), inplace=True)
df['OutletSize'].fillna(df['OutletSize'].mode()[0], inplace=True)

# ----- categorical cleansing -----
df['FatContent'].exchange(
    {'low fats': 'Low Fats', 'LF': 'Low Fats', 'reg': 'Common'},
    inplace=True
)

# ----- classification goal -----
threshold = df['OutletSales'].median()
df['SalesCategory'] = (df['OutletSales'] > threshold).astype(int)

# ----- one-hot encode categoricals -----
cat_cols = [
    'FatContent', 'ProductType', 'OutletID',
    'OutletSize', 'LocationType', 'OutletType'
]
df = pd.get_dummies(df, columns=cat_cols, drop_first=True)

# ----- cut up options / labels -----
X = df.drop(['ProductID', 'OutletSales', 'SalesCategory'], axis=1).values
y = df['SalesCategory'].values

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=SEED, stratify=y
)

scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.rework(X_test)

# create torch tensors
X_train_t = torch.tensor(X_train, dtype=torch.float32)
y_train_t = torch.tensor(y_train, dtype=torch.lengthy)
X_test_t = torch.tensor(X_test, dtype=torch.float32)
y_test_t = torch.tensor(y_test, dtype=torch.lengthy)

# cut up prepare into prepare/val (80/20 of authentic prepare)
val_frac = 0.2
val_size = int(len(X_train_t) * val_frac)
train_size = len(X_train_t) - val_size

train_ds, val_ds = random_split(
    TensorDataset(X_train_t, y_train_t),
    [train_size, val_size],
    generator=torch.Generator().manual_seed(SEED)
)

train_loader = DataLoader(
    train_ds, batch_size=64, shuffle=True, drop_last=True
)
val_loader = DataLoader(
    val_ds, batch_size=256, shuffle=False
)

Customized Loss: Within the 2nd step, first, we’ll create a customized SalesClassifier. Contemplate that we apply Focal Loss to put extra emphasis on the minority class. Then, we’ll refit the mannequin to maximise Focal Loss as an alternative of Cross Entropy Loss. In lots of instances, the Focal Loss will increase recall on the minor class however might lower uncooked accuracy. After that, we’ll prepare our gross sales classifier with the assistance of the customized SoftF1Loss over 100 epochs and save one of the best mannequin as best_model.pt

class SalesClassifier(nn.Module):

   def __init__(self, input_dim):

       tremendous().__init__()

       self.web = nn.Sequential(

           nn.Linear(input_dim, 128),

           nn.BatchNorm1d(128),

           nn.ReLU(inplace=True),

           nn.Dropout(0.5),

           nn.Linear(128, 64),

           nn.ReLU(inplace=True),

           nn.Dropout(0.25),

           nn.Linear(64, 2)          # logits for two lessons

       )

   def ahead(self, x):

       return self.web(x)

# class-weighted CrossEntropy to battle imbalance

class_weights = compute_class_weight('balanced',

                                    lessons=np.distinctive(y_train),

                                    y=y_train)

class_weights = torch.tensor(class_weights, dtype=torch.float32,

                            system=system)

ce_loss = nn.CrossEntropyLoss(weight=class_weights)

Right here, we’ll be utilizing a customized loss operate named SoftF1Loss. So right here the SoftF1Loss is a customized loss operate that straight optimizes for the F1-score in a differentiable method, making it appropriate for gradient-based coaching. As an alternative of utilizing exhausting 0/1 predictions, it really works with gentle chances from the mannequin’s output (torch.softmax), so the loss adjustments easily as predictions change. It calculates the gentle true positives (TP), false positives (FP), and false negatives (FN) utilizing these chances and the true labels, then computes gentle precision and recall. From these, it derives a “gentle” F1-score and returns 1 – F1 in order that minimizing the loss will maximize the F1-score. That is particularly helpful when coping with imbalanced datasets the place accuracy isn’t a great measure of efficiency.

# Differentiable Customized Loss Perform Gentle-F1 loss

class SoftF1Loss(nn.Module):

   def ahead(self, logits, labels):

       probs = torch.softmax(logits, dim=1)[:, 1]   # positive-class prob

       labels = labels.float()

       tp = (probs * labels).sum()

       fp = (probs * (1 - labels)).sum()

       fn = ((1 - probs) * labels).sum()

       precision = tp / (tp + fp + 1e-7)

       recall    = tp / (tp + fn + 1e-7)

       f1 = 2 * precision * recall / (precision + recall + 1e-7)

       return 1 - f1

f1_loss = SoftF1Loss()

def total_loss(logits, targets, alpha=0.5):

   return alpha * ce_loss(logits, targets) + (1 - alpha) * f1_loss(logits, targets)

mannequin = SalesClassifier(X_train.form[1]).to(system)

optimizer = torch.optim.Adam(mannequin.parameters(), lr=1e-3)

best_val = float('inf'); endurance=10; patience_cnt=0

for epoch in vary(1, 101):

   mannequin.prepare()

   train_losses = []

   for xb, yb in train_loader:

       xb, yb = xb.to(system), yb.to(system)

       optimizer.zero_grad()

       logits = mannequin(xb)

       loss = total_loss(logits, yb)

       loss.backward()

       optimizer.step()

       train_losses.append(loss.merchandise())

   # ----- validation -----

   mannequin.eval()

   with torch.no_grad():

       val_losses = []

       for xb, yb in val_loader:

           xb, yb = xb.to(system), yb.to(system)

           val_losses.append(total_loss(mannequin(xb), yb).merchandise())

       val_loss = np.imply(val_losses)

   if epoch % 10 == 0:

       print(f'Epoch {epoch:3d} | TrainLoss {np.imply(train_losses):.4f}'

             f' | ValLoss {val_loss:.4f}')

   # ----- early stopping -----

   if val_loss < best_val - 1e-4:

       best_val = val_loss

       patience_cnt = 0

       torch.save(mannequin.state_dict(), 'best_model.pt')

   else:

       patience_cnt += 1

       if patience_cnt >= endurance:

           print('Early stopping!')

           break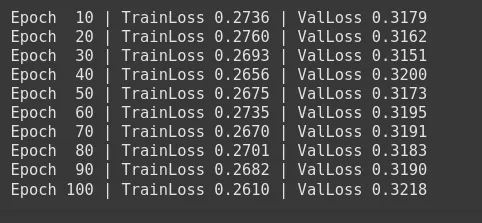

# load greatest weights

mannequin.load_state_dict(torch.load('best_model.pt'))

Calibration Earlier than/After: On this stream, we might have discovered that the ECE for the baseline mannequin was excessive, indicating the mannequin was overconfident. So the  Anticipated Calibration Error (ECE) for the baseline mannequin could also be excessive/low, indicating the mannequin was overconfident/underconfident. 

We will now calibrate the mannequin utilizing temperature scaling after which repeat the method to calculate a brand new ECE and plot a brand new reliability curve. We are going to see that the reliability curve might transfer nearer to the diagonal after temperature scaling happens.

class ModelWithTemperature(nn.Module):

   def __init__(self, mannequin):

       tremendous().__init__()

       self.mannequin = mannequin

       self.temperature = nn.Parameter(torch.ones(1) * 1.5)

   def ahead(self, x):

       logits = self.mannequin(x)

       return logits / self.temperature

model_ts = ModelWithTemperature(mannequin).to(system)

optim_ts = torch.optim.LBFGS([model_ts.temperature], lr=0.01, max_iter=50)

def _nll():

   optim_ts.zero_grad()

   logits = model_ts(X_val := X_test_t.to(system))   # use check set to suit T

   loss = ce_loss(logits, y_test_t.to(system))

   loss.backward()

   return loss

optim_ts.step(_nll)

print('Optimum temperature:', model_ts.temperature.merchandise())

Optimum temperature: 1.585491418838501

Visualization: On this part, we’ll be plotting reliability diagrams “earlier than” and “after” calibration. The diagrams are a visible illustration of the improved alignment.

@torch.no_grad()

def get_probs(mdl, X):

   mdl.eval()

   logits = mdl(X.to(system))

   return F.softmax(logits, dim=1).cpu()

def ece(probs, labels, n_bins=10):

   conf, preds = probs.max(1)

   accs = preds.eq(labels)

   bins = torch.linspace(0,1,n_bins+1)

   ece_val = torch.zeros(1)

   for lo, hello in zip(bins[:-1], bins[1:]):

       masks = (conf>lo) & (conf<=hello)

       if masks.any():

           ece_val += torch.abs(accs[mask].float().imply() - conf[mask].imply()) 

                      * masks.float().imply()

   return ece_val.merchandise()

def plot_reliability(ax, probs, labels, n_bins=10, label="Mannequin"):

   conf, preds = probs.max(1)

   accs = preds.eq(labels)

   bins = torch.linspace(0,1,n_bins+1)

   bin_acc, bin_conf = [], []

   for i in vary(n_bins):

       masks = (conf>bins[i]) & (conf<=bins[i+1])

       if masks.any():

           bin_acc.append(accs[mask].float().imply().merchandise())

           bin_conf.append(conf[mask].imply().merchandise())

   ax.plot(bin_conf, bin_acc, marker="o", label=label)

   ax.plot([0,1],[0,1],'--',shade="orange")

   ax.set_xlabel('Confidence'); ax.set_ylabel('Accuracy')

   ax.set_title('Reliability Diagram'); ax.grid(); ax.legend()

probs_before = get_probs(mannequin   , X_test_t)

probs_after  = get_probs(model_ts, X_test_t)

print('nClassification report (calibrated logits):')

print(classification_report(y_test, probs_after.argmax(1)))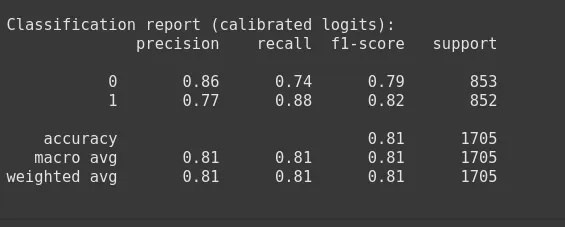

print('ECE earlier than T-scaling :', ece(probs_before, y_test_t))

print('ECE after  T-scaling :', ece(probs_after , y_test_t))

#----------------------------------------

# ECE earlier than T-scaling : 0.05823298543691635

# ECE after  T-scaling : 0.02461853437125683

# ----------------------------------------------

# reliability plot

fig, ax = plt.subplots(figsize=(6,5))

plot_reliability(ax, probs_before, y_test_t, label="Earlier than T-Scaling")

plot_reliability(ax, probs_after , y_test_t, label="After  T-Scaling")

plt.present()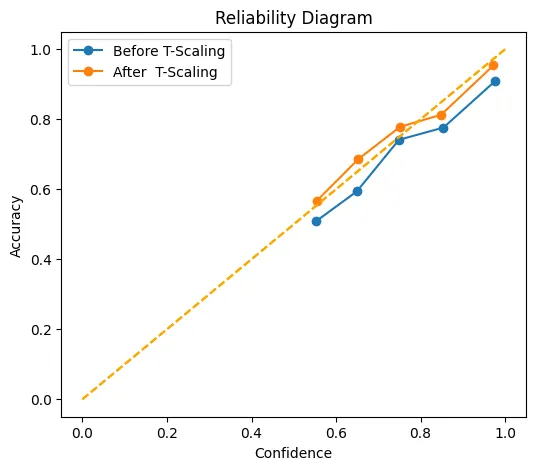

This chart reveals how nicely the boldness rating matches/aligns with the precise values, each earlier than (blue) and after (orange) temperature scaling. The x-axis displays their imply said confidence, whereas the y-axis displays how incessantly these predictions have been scored correctly. The dotted diagonal line represents good calibration factors that coincide with this line, representing.

For instance, predictions which can be scored with 70% confidence are appropriately scored 70% of the time. After scaling, the orange line hugs this diagonal line extra intently than the blue line does. Particularly within the ‘center’ of the boldness area between 0.6 and 0.9 confidence, and nearly meets the perfect level at (1.0, 1.0). In different phrases, temperature scaling has the potential to scale back the mannequin’s proclivity towards over- or under-confidence in order that its level estimates of the likelihood are significantly extra correct.

Examine the whole pocket book here.

Conclusion

In real-world AI purposes, validity and calibration are equally essential. A mannequin might have excessive validity, but when the mannequin’s confidence shouldn’t be correct, then there’s little worth in having greater validity. Due to this fact, creating customized loss capabilities specific to your downside assertion through the coaching can match our true aims, and we consider calibration so we are able to interpret predictive chances appropriately. 

Due to this fact full analysis technique considers each: we first enable the customized losses to completely optimize the mannequin for the duty, after which we deliberately calibrate and validate the likelihood outputs. Now we are able to create a decision-support software, the place a “90% confidence” actually is “90% seemingly,” which is essential for any real-world implementation.

Learn extra: Prime 7 Loss capabilities for Regression fashions

Continuously Requested Questions